الگوریتم دایکسترا یکی از مهمترین و پرکاربردترین الگوریتمهای گراف است که برای یافتن مسیر کوتاهترین بین یک راس مبدأ به تمامی رئوس گراف متصل استفاده میشود. این الگوریتم اسم خود را از نام عالم ریاضی و مخترع این الگوریتم، یعنی “ادسگر دایکسترا”، به ارث برده است. در این مقاله، به بررسی جزئیات عملکرد، اصول و کاربردهای الگوریتم دایکسترا در مسائل گوناگون پرداختهایم.
مقدمه
الگوریتم دایکسترا یک الگوریتم مهم و کارآمد برای حل مسائل مربوط به مسائل جستجوی مسیر در گرافها است. این الگوریتم به عنوان یکی از الگوریتمهای کلیدی در حوزه مسائل مسیریابی و شبکهها مورد استفاده قرار میگیرد. مسئلهای که الگوریتم دایکسترا حل میکند، یافتن مسیر کوتاهترین بین یک نقطه مبدأ به تمامی نقاط دیگر گراف است، با فرض اینکه وزن یالها مثبت باشند.
عملکرد الگوریتم دایکسترا
الگوریتم دایکسترا با استفاده از یک رویکرد حریصانه (greedy) عمل میکند. این الگوریتم به ازای هر راس، مسافت کوتاهترین فاصله را از راس مبدأ محاسبه میکند و سپس به تدریج مسافتهای را از راس مبدأ به رئوس دیگر گراف به روز میکند. در هر مرحله، راسی که دارای کمترین مسافت از راس مبدأ باشد و هنوز مورد بررسی قرار نگرفته باشد، به عنوان راس کنونی انتخاب میشود و مسافتها بهروزرسانی میشود. این فرآیند تا زمانی که همه رئوس مورد بررسی قرار گیرند ادامه مییابد.
مراحل عملکرد
الگوریتم دایکسترا شامل مراحل زیر است:
- مقداردهی اولیه: مسافت هر راس از راس مبدأ را برابر بینهایت قرار دهید، مگر اینکه خود راس مبدأ باشد که مسافت آن را صفر قرار دهید.
- انتخاب راس کنونی: انتخاب راسی که مسافت کمترین فاصله تا آن از راس مبدأ باشد و هنوز مورد بررسی قرار نگرفته باشد.
- به روزرسانی مسافتها: مسافتهای تمام رئوس مجاور راس کنونی را با استفاده از مسافت راس کنونی و وزن یالها به روزرسانی کنید.
- علامتگذاری راس کنونی: راس کنونی را علامتگذاری کرده و آن را از لیست رئوس مورد نظر خارج کنید.
- تکرار مراحل: مراحل 2 تا 4 را تا زمانی که همه رئوس بررسی شوند انجام دهید.
مثال
برای بهترین درک از عملکرد الگوریتم دایکسترا، بیایید یک مثال ساده را بررسی کنیم:
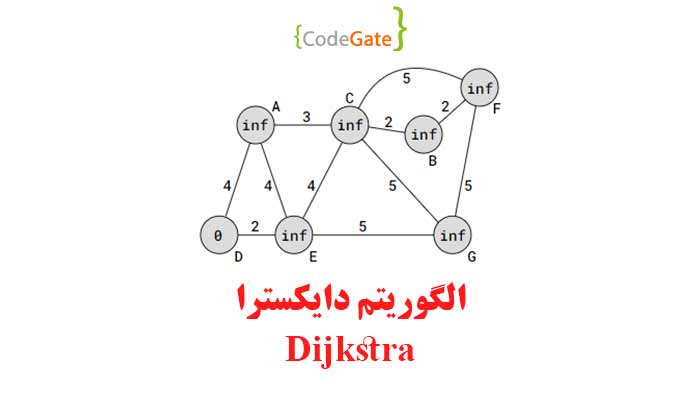
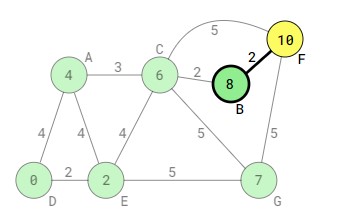
فرض کنید ما یک گراف با رئوس و یالهای زیر داشته باشیم:
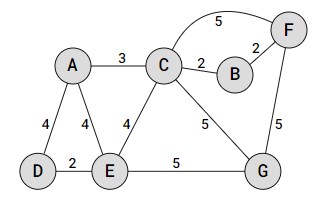
در این گراف، هر یال مجهز به وزنی است که نشاندهنده فاصله بین رئوس متصل است. ما میخواهیم مسیر کوتاهترین از راس A به تمامی رئوس دیگر گراف را پیدا کنیم. با استفاده از الگوریتم دایکسترا، مراحل به صورت زیر انجام میشود:
- مقداردهی اولیه: مسافت هر راس از راس مبدأ (A) برابر بینهایت قرار میگیرد، مگر راس مبدأ که مسافت آن صفر است.
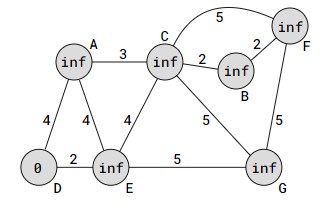
انتخاب راس کنونی: راس D به عنوان راس کنونی انتخاب میشود.
بهروزرسانی مسافتها: مسافتهای رئوس مجاور D(یعنی A، وE) با توجه به مسافت D و وزن یالها به روزرسانی میشود. فاصله D تا E برابر با 2 است همچنین فاصله D تا A برابر با 4 است پس مقدار بی نهایت (inf) راس های E و A تغییر میکند.
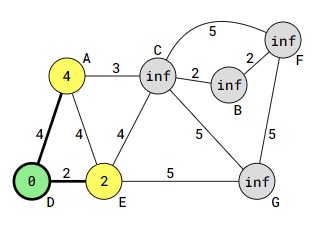
علامتگذاری راس کنونی: راس A علامتگذاری میشود و راس ملاقات گردیده (visited) در نظر گرفته خواهد شد.
تکرار مراحل: مراحل 2 تا 5 با رئوس بعدی انجام میشود.
انتخاب راس کنونی: راس E به عنوان راس کنونی انتخاب میشود.
بهروزرسانی مسافتها: مسافتهای رئوس مجاور E(یعنی A، وC و G) با توجه به مسافت E و وزن یالها به روزرسانی میشود. در این مرحله ما باید فاصله راس شروع (D) را تا راسهای A و C و G بدست آوریم.فاصله E تا A برابر با 4 است و فاصله D تا E برابر با 2 پس فاصله D تا A از مسیر راس E برابر با 4+2 میشود. راس A از مسیر دیگری که در مرحله قبل رفتیم فاصله برابر با 4 دارد. پس فاصله جدید که 6 است جایگزین نمیشود و همان مسیر قبلی کوتاهترین مسیر است. برای راسهای C و G نیز همین کار را میکنیم. مسافت مبدا (D) تا C برابر با 2+4 و مسافت مبدا تا G برابر با 2+5 میباشد. این دو مسافت جایگزین مقدار inf میشوند.
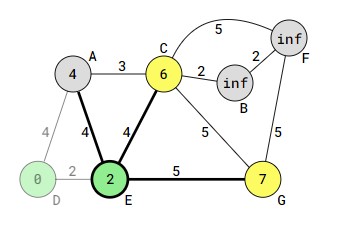
- راس E نیز visited علامتگذاری میشود
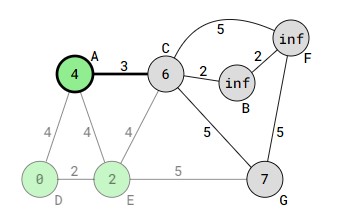
- مراحله بعد راس A، راس کنونی میباشد:
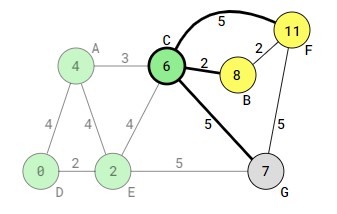
- مراحل بررسی راسها را ادامه میدهیم تا همگی راسها visited شوند
کاربردهای الگوریتم دایکسترا
الگوریتم دایکسترا به عنوان یکی از ابزارهای اساسی در حوزه مسائل مسیریابی و شبکهها مورد استفاده قرار میگیرد. برخی از کاربردهای این الگوریتم عبارتند از:
- مسائل مسیریابی در شبکهها: برای یافتن مسیر کوتاهترین بین دو نقطه در یک شبکه، مانند مسائل مرتبط با شبکههای مخابراتی یا مسائل مسیریابی در اینترنت.
- مسائل مسیریابی در حمل و نقل: برای برنامهریزی مسیریابی خودروها، هواپیماها یا هر وسیله حمل و نقل دیگر.
- بهینهسازی شبکههای ارتباطی: برای بهینهسازی مسیرهای ارتباطی در شبکههای اجتماعی، شبکههای اطلاعاتی، یا سیستمهای پردازش ابری.
نتیجهگیری
الگوریتم دایکسترا یکی از الگوریتمهای کارآمد و مفید در حوزه مسائل گراف است که در بسیاری از حوزههای علوم کامپیوتر و مهندسی مورد استفاده قرار میگیرد. با استفاده از اصول و مراحل عملکرد این الگوریتم، میتوان به بهترین شیوه ممکن از آن برای حل مسائل مختلف استفاده کرد و به نتایج دقیق و مطلوب دست یافت.