در این قسمت تیم کدگیت را با آموزش جستجوی اول سطح (BFS) در پایتون همراهی کنید. در دو آموزش گذشته در خصوص نحوه پیاده سازی گراف غیر جهت دار و جهتدار صحبت شد. در این جلسه با استفاده از پیادهسازی گرافها در پایتون، جستجوی اول سطح را توضیح خواهیم داد. پیشنیازهای این جلسه، آموزشهای زیر میباشد:
- گراف در پایتون
- گراف جهت دار در پایتون
- تابع در پایتون
- حلقه for در پایتون
- حلقه While در پایتون
- دیکشنری در پایتون
- لیست در پایتون
- شی گرایی در پایتون
- If در پایتون
BFS
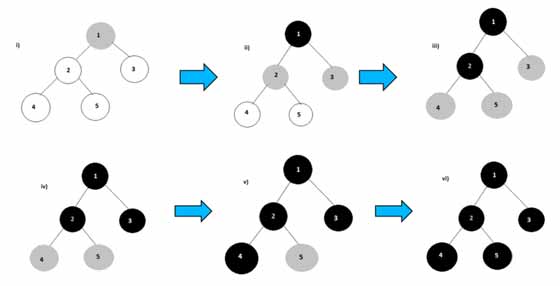
در نظریه گراف، جستجوی اول سطح یکی از الگوریتم پیمایش گراف است. استراتژی جستجوی سطح اول برای پیمایش گراف، همانطور که از نامش پیداست «جستجوی سطح به سطح گراف» است.
الگوریتم از ریشه شروع میکند (در گرافها و یا درختهای بدون ریشه رأس دلخواهی به عنوان ریشه انتخاب میشود) و آن را در سطح یک قرار میدهد. سپس در هر مرحله همه همسایههای رئوس آخرین سطح دیده شده را که تا به حال دیده نشدهاند بازدید میکند و آنها را در سطح بعدی میگذارد. این فرایند زمانی متوقف میشود که همه همسایههای رئوس آخرین سطح قبلاً دیده شده باشند.
از نقطه نظر عملی، برای پیادهسازی این الگوریتم از صف استفاده میشود. بدین ترتیب که در ابتدا ریشه در صف قرار میگیرد. سپس هر دفعه عنصر ابتدای صف بیرون کشیده شده، همسایگانش بررسی شده و هر همسایهای که تا به حال دیده نشده باشد به انتهای صف اضافه میشود. جزئیات پیادهسازی در ادامه خواهد آمد.
جستجوی اول سطح در پایتون
برای پیاده سازی جستجوی اول سطح در پایتون همانطور که گفته شد از صف استفاده میکنند. در پایتون از ساختار داده لیست (List) که ویژگیهای یک صف را دارد استفاده میکنیم. در آموزش گذشته پیاده سازی گراف را انجام دادهایم و از همان پیادهسازی برای این آموزش استفاده میشود.متدهای addEdge برای اضافه کردن گراف، V تعداد گره ها، edge برای تعداد یالها و printGraph برای نمایش گراف پیاده سازی شده است. کد گرافی که در جلسه گذشته پیاده سازی کردیم به صورت زیر است:
from collections import defaultdict
class UnDirectedGraph:
# Constructor
def __init__(self):
# default dictionary to store graph
self.graph = defaultdict(list)
self.E = 0
# function to add an edge to graph
def addEdge(self,u,v):
if v in self.graph[u]:
return
if u == v:
self.graph[u].append(v)
return
self.graph[u].append(v)
self.graph[v].append(u)
self.E+=1
def V(self):
return len(self.graph)
def Edge(self):
return self.E
def printGraph(self):
for i in self.graph:
print(i,':',end=' ')
for j in self.graph[i]:
print(j, end= ' ')
print()
یک متد با نام BFS ایجاد میکنیم. ورودی این متد، نقطه آغاز الگوریتم یا همان گره ریشه میباشد. سپس یک ساختار داده لیست (به نام visited)به طول گرههای گراف میسازیم. در صورتی که گرهای را بررسی کردیم مقدار آن برابر با True میشود. کد این قسمت به صورت زیر است:
def BFS(self, s):
visited = [False] * (max(self.graph) + 1)
حال نوبت به پیاده سازی الگوریتم میرسد. ابتدا لیستی به نام queue ایجاد و ریشه(متغیر s) را وارد آن میکنیم. مقدار Visited برای ریشه نیز True میکنیم:
queue = []
# Mark the source node as
# visited and enqueue it
queue.append(s)
visited[s] = True
حال تا زمانی که صف خالی نشده است گره که در اول صف قرار دارد را از صف خارج کرده و همسایههای آن را وارد صف میکنیم (البته اگر قبلا آن را بررسی نکرده باشیم). کد این قسمت به صورت زیر میباشد:
while queue:
# Dequeue a vertex from
# queue and print it
s = queue.pop(0)
print (s, end=" ")
# Get all adjacent vertices of the
# dequeued vertex s. If a adjacent
# has not been visited, then mark it
# visited and enqueue it
for i in self.graph[s]:
if visited[i] == False:
queue.append(i)
visited[i] = True
تست جستجوی اول سطح در پایتون
برای تست کدهای بالا، main زیر را اجرا کنید:
if __name__ == '__main__':
g = UnDirectedGraph()
g.addEdge(0, 1)
g.addEdge(0, 4)
g.addEdge(1, 4)
g.addEdge(1, 3)
g.addEdge(1, 2)
g.addEdge(2, 3)
g.addEdge(3, 4)
print('print Graph:')
g.printGraph()
print('BFS:',end=' ')
g.BFS(0)
print()
گراف ورودی به صورت زیر میباشد:
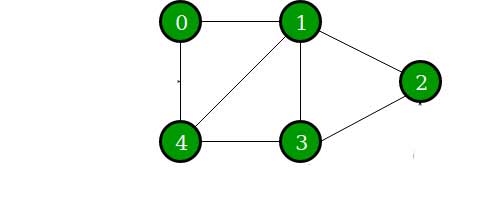
خروجی برنامه نیز به صورت زیر است:
print Graph:
0 : 1 4
1 : 0 4 3 2
4 : 0 1 3
3 : 1 2 4
2 : 1 3
BFS: 0 1 4 3 2