در این آموزش تیم کدگیت را با توضیح هیپ (heap) یا هرم در جاوا همراهی کنید. برای درک بهتر این آموزش پیشنهاد می شود آموزش های قبلی ساختمان داده مانند لینک لیست یا پشته را مطالعه کنید.
هیپ (Heap)
در علوم رایانه، هرم یا هیپ (heap) یک ساختمان دادهی درخت (ساختار داده) است که شرط «اگر B بچه A بود، آنگاه مقدار گره A بزرگتر مساوی مقدار گره B باشد» را ارضا کند. این مسئله بیانگر این است که گره با بیشترین مقدار همواره در ریشه قرار میگیرد و بنابراین چنین هیپی، هیپ بیشینه نامیده میشود. بر روی این که هر گره چند گره فرزند داشته باشد، هیچ محدودیتی وجود ندارد، حال آنکه در عمل معمولاً هر گره، دو فرزند دارد. هیپ یک داده ساختار بهینه برای پیادهسازی یک داده انتزاعی به نام صف اولویت دار میباشد. هیپها در الگوریتمهای زیادی مانند الگوریتم دیکسترا در نظریه گراف کاربرد دارند(ویکیپدیا).
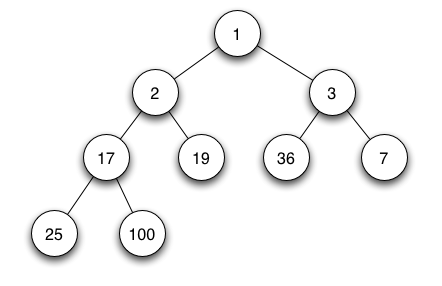
درخت دودویی کامل
یک درخت دودویی کامل است، هرگاه تمامی سطوح درخت به غیر از احتمالا آخرین سطح پر بوده و برگهای سطح آخر از سمت چپ قرار گرفته باشند.
هرم دودویی
هرم دودویی یک دادهساختار هرم است که از یک درخت دودویی استفاده میکند. میتوان به این دادهساختار به عنوان یک درخت دودویی نگاه کرد با این تفاوت که باید دو محدودیت را در نظر بگیریم. اول اینکهای درخت، درخت دودویی کامل است، در همه سطحهای این درخت این ویژگی برقرار است به جز احتمالاً سطح اخر که در سطح اخر گرهها از چپ به راست پر هستند (خاصیت ظاهری). و مورد دوم اینکه همه گرهها از فرزندشان کوچکتر مساوی (یا بزرگترمساوی) هستند. اگر همه گرهها از فرزندانشان کوچکتر مساوی باشند هرم کمینه و اگر همه گرهها بزرگتر مساوی از فرزندانشان باشند هرم بیشینه نامگذاری میشوند (خاصیت هرم). اغلب برای پیادهسازی صف اولویت از هرم کمینه استفاده میشود.
نمایش هرم دودویی
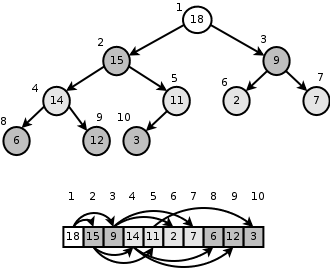
هرم دودویی اگر بخواهیم با لیست پیوندی نمایش دهیم نیاز به سه اشاره گر داریم برای جست و جوی رو به پایین و رو به بالا(هر نود به فرزندان خود و پدرش اشاره دارد) پیاده سازی این کار ساده است ولی همیشه یک درخت دودویی کامل ما را به یاد آرایه می اندازد و از این رو پیاده سازی هرم با آرایه کاره ساده تری است. با آرایه دیگر ما از اشاره گر استفاده نمیکنیم و کل کار ما با اندیس آرایه است. برای نمایش هرم دودویی، اگر نودی در خانه i بود فرزندان آن در خانه 2i+1 و 2i هستند.
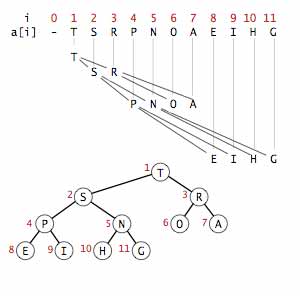
پیاده سازی هیپ بیشینه
برای پیاده سازی هرم بیشینه ابتدا به توضیح متد های کمکی این کار میپردازیم و سپس به طور کامل آن را پیاده سازی میکنیم.
متدهای less و exch برای مقایسه و جابجایی دو نود از هرم استفاده میشود.
private boolean less(int i, int j) {
return ((Comparable<Key>) pq[i]).compareTo(pq[j]) < 0;
}
private void exch(int i, int j) {
Key swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
}
متد swim زمانی استفاده میشود که نودی از پدرش بزرگتر شود و ما نیاز داریم تا شرط هرم بیشینه را رعایت کنیم به همین دلیل باید مکان مناسبی برای این نود در درخت ایجاد شده پیدا کنیم و هیچ شرطی هم نقض نشود. ما نود بزرگتر را با پدرش جابجا میکنیم و اگر نود جابجا شده از تمام فرزندان بزرگتر بود ممکن است دوباره مشکل اول برای ما پیش بیاید یعنی نودی که جابجا کردیم از پدرش بزرگتر باشد پس همین کار را ادامه میدهیم تا دیگر نتوانیم جابجایی انجام دهیم.متد swim این کار را انجام میدهد.
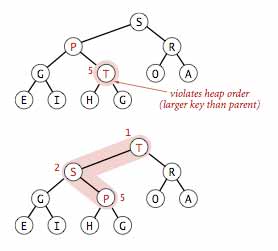
private void swim(int k) {
while (k > 1 && less(k / 2, k)) {
exch(k, k / 2);
k = k / 2;
}
}
متد sink موقعی استفاده میشد که نود پدر از فرزندانش کوچکتر باشد. در این صودت ما باید مکانی برای این نود پیدا کنیم که شرط هرم نقض نشود. برای این کار ما نود پدر را با بزرگترین نود فرزند جا به جا میکنیم و اگر دوباره اتفاق بزرگ بودن پدر رخ داد، همین جابجایی را انجام میدهیم تا دیگر نتوانیم نودی را جابجا کنیم. کاره متد sink این است.

private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1))
j++;
if (!less(k, j))
break;
exch(k, j);
k = j;
}
}
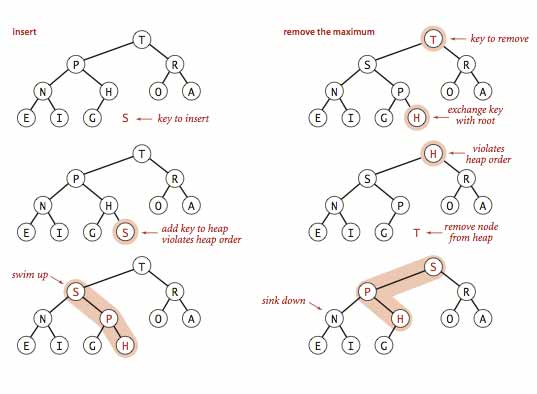
حال دو متد insert و remove max را توضیح میدهیم. متد insert یک نود را به هرم اضافه میکند برای این کار ما یک نود به آخر آرایه اضافه میکنیم و متد swim که توضیح داده شد را صدا میزنیم تا شرط هیپ برقرار باشد. کاری که متد remove max انجام میدهد این است که به جای نود اول نود آخر قرار میدهد و متد sink را صدا میزند تا دوباره هیپ ساخته شود.
public void insert(Key x) {
if (N >= pq.length - 1)
resize(2 * pq.length);
pq[++N] = x;
swim(N);
}
public Key delMax() {
if (isEmpty())
throw new NoSuchElementException("Priority queue underflow");
Key max = pq[1];
exch(1, N--);
sink(1);
pq[N + 1] = null; // to avoid loiterig and help with garbage collection
if ((N > 0) && (N == (pq.length - 1) / 4))
resize(pq.length / 2);
return max;
}
حال به پیاده سازی هرم بیشینه میپردازیم. کل کد در یک کلاس به نام maxheap مینویسیم.
import java.util.Comparator;
import java.util.Iterator;
import java.util.NoSuchElementException;
import java.util.Spliterator;
import java.util.function.Consumer;
public class MaxHeap<Key> implements Iterable<Key> {
private Key[] pq; // store items at indices 1 to N
private int N; // number of items on priority queue
public MaxHeap(int capacity) {
pq = (Key[]) new Object[capacity + 1];
N = 0;
}
public MaxHeap() {
this(1);
}
public boolean isEmpty() {
return N == 0;
}
public int size() {
return N;
}
public Key max() {
if (isEmpty())
throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
private void resize(int capacity) {
assert capacity > N;
Key[] temp = (Key[]) new Object[capacity];
for (int i = 1; i <= N; i++)
temp[i] = pq[i];
pq = temp;
}
public void insert(Key x) {
if (N >= pq.length - 1)
resize(2 * pq.length);
pq[++N] = x;
swim(N);
}
public Key delMax() {
if (isEmpty())
throw new NoSuchElementException("Priority queue underflow");
Key max = pq[1];
exch(1, N--);
sink(1);
pq[N + 1] = null; // to avoid loiterig and help with garbage collection
if ((N > 0) && (N == (pq.length - 1) / 4))
resize(pq.length / 2);
return max;
}
private void swim(int k) {
while (k > 1 && less(k / 2, k)) {
exch(k, k / 2);
k = k / 2;
}
}
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1))
j++;
if (!less(k, j))
break;
exch(k, j);
k = j;
}
}
private void exch(int i, int j) {
Key swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
}
// is pq[1..N] a max heap?
private boolean isMaxHeap() {
return isMaxHeap(1);
}
// is subtree of pq[1..N] rooted at k a max heap?
private boolean isMaxHeap(int k) {
if (k > N)
return true;
int left = 2 * k, right = 2 * k + 1;
if (left <= N && less(k, left))
return false;
if (right <= N && less(k, right))
return false;
return isMaxHeap(left) && isMaxHeap(right);
}
private boolean less(int i, int j) {
return ((Comparable<Key>) pq[i]).compareTo(pq[j]) < 0;
}
public Iterator<Key> iterator() {
return new HeapIterator();
}
private class HeapIterator implements Iterator<Key> {
// create a new pq
private MaxHeap<Key> copy;
// add all items to copy of heap
// takes linear time since already in heap order so no keys move
public HeapIterator() {
copy = new MaxHeap<Key>(size());
for (int i = 1; i <= N; i++)
copy.insert(pq[i]);
}
public boolean hasNext() {
return !copy.isEmpty();
}
public void remove() {
throw new UnsupportedOperationException();
}
public Key next() {
if (!hasNext())
throw new NoSuchElementException();
return copy.delMax();
}
}
public static void main(String[] args) {
MaxHeap<String> pq = new MaxHeap<String>();
String list[] ={"A","B","C","D","E"};
for (int i = 0; i < list.length; i++) {
pq.insert(list[i]);
}
Iterator it = pq.iterator();
while (it .hasNext()) {
String type = (String) it.next();
System.out.println(type);
}
}
}
خروجی کد بالا به صورت زیر است:
E
D
C
B
A














