ترانهاده و ضرب ماتریس در جاوا (Matrix)

در این جلسه، تیم کدگیت را با  آموزش ترانهاده و ضرب ماتریس در جاوا همراهی کنید. پیش نیاز این جلسه، آشنایی با آرایه و کار با آن است.

ماتریس

ماتریس به آرایشی مستطیلی شکل از اعداد یا عبارات ریاضی که بصورت سطر و ستون شکل یافته گفته می‌شود. به طوری که می‌توان گفت که هر ستون یا هر سطر یک ماتریس، یک بردار را تشکیل می‌دهد. هر یک از عناصر ماتریس درایه خوانده می‌شود. ماتریسی با ۲ سطر و ۳ ستون به این شکل است:

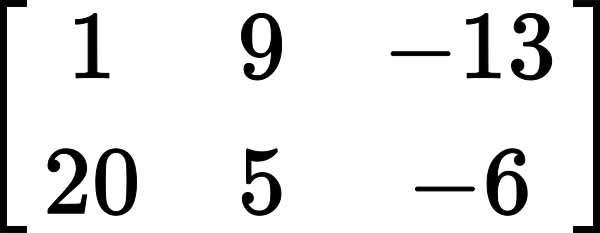
ماتریس‌های هم اندازه (با تعداد سطر و ستون برابر) را می‌توان با هم جمع یا از هم تفریق کرد. ضرب دو ماتریس تنها در صورتی ممکن است که تعداد ستون‌های ماتریس اول با تعداد سطرهای ماتریس دوم برابر باشد.

در جبر خطی، می‌توان اثبات کرد که هر نگاشت خطیِ، از فضای Rⁿ به فضای Rⁿ ، یک‌ریخت با یک ماتریس m*n (یعنی m سطر n ستون) می‌باشد. ماتریس‌ها کاربردهای فراوانی در جبر خطی دارند(ویکیپدیا).

ضرب ماتریس ها

ضرب معمولی ماتریس‌ها رایج‌ترین نوع ضرب در ماتریس‌هاست. این نوع ضرب تنها زمانی تعریف می‌شود که تعداد ستون‌های ماتریس اول با تعداد سطرهای ماتریس دوم برابر باشد. حاصل‌ضرب یک ماتریس mدرn در یک ماتریس nدرp یک ماتریس mدرp است، به همین صورت اگر لیستی از ماتریس‌ها برای ضرب را داشته باشیم که ابعاد مختلفی دارند(مانند mدرn ، nدرp ، pدرq ، qدرr ) بُعد ماتریس حاصل ضرب از تعداد سطرهای اولین ماتریس و تعداد ستون‌های آخرین ماتریس می‌آید (مثلاً در لیست ذکر شده در بالا بعد ماتریس حاصلضرب mدرr خواهد بود). توجه به این نکته نیز لازم است که ضرب ماتریس‌ها خاصیت جابجایی ندارد.

ضرب معمولی به این صورت تعریف می‌شود

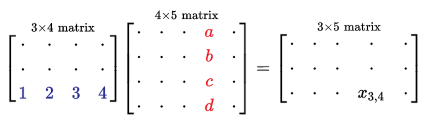
که در آن درایه X_3,4 برابر است با :

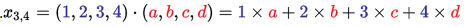
ترانهاده ماتریس

در جبر خطی ترانهاده یک ماتریس مانند A ماتریس دیگری است که با نماد A^T مشخص شده و نسبت به ماتریس A دارای تفاوت با تعریف زیر است:

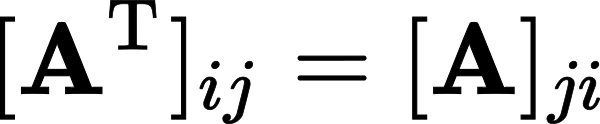
به عبارت دیگر باید هنگام نوشتن ترانهاده هر ماتریسی سطرهای ماتریس را به شکل ستون نوشت و ستون‌های ماتریس را به شکل سطر در واقع یک ماتریس n×m اگر ترانهاده شود یک ماتریس m×n خواهد بود.ترانهاده یک عدد همان عدد است.(ویکیپدیا)

پیاده سازی ترانهاده و ضرب ماتریس در جاوا

برای پیاده سازی ترانهاده و ضرب ماتریس در جاوا از آرایه استفاده میکنیم. به این صورت که هر ماتریس را یک آرایه دو بعدی می

گیریم و سپس عملیات ترانهاده و ضرب را انجام میدهیم.

یک کلاس به نام Matrix میسازیم. و کد زیر را در آن قرار میدهیم.

public class Matrix {

// return C = A^T
public static double[][] transpose(double[][] A) {
int m = A.length;
int n = A[0].length;
double[][] C = new double[n][m];
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
C[j][i] = A[i][j];
return C;
}


// return C = A * B
public static double[][] multiply(double[][] A, double[][] B) {
int mA = A.length;
int nA = A[0].length;
int mB = B.length;
int nB = B[0].length;
if (nA != mB)
throw new RuntimeException("Illegal matrix dimensions.");
double[][] C = new double[mA][nB];
for (int i = 0; i < mA; i++)
for (int j = 0; j < nB; j++)
for (int k = 0; k < nA; k++)
C[i][j] += A[i][k] * B[k][j];
return C;
}

}

کد ترانهاده و ضرب ماتریس در جاوا شامل متدهای زیر است:

1. Transpose: متدی که یک آرایه میگیرد و خروجی به ما ترانهاده ماتریس میدهد.
2. Multiply: متدی که دو ماتریس را میگیرد و حاصلضرب آن ها را برمیگرداند.

در متد multiply ابتدا ابعاد ماتریس را میگیریم و چک میکنیم که دو ماتریس را میتوان ضرب کرد یا خیر. اگر بتوانیم ضرب کنیم باید برای هر درایه ماتریس حاصلضرب، سطر خاص از  ماتریس اول در ستون خاص از ماتریس دوم ضرب کنیم به همین دلیل باید علاوه بر 2 حلقه for که به تعداد سطر و ستونهای ماتریس حاصلضرب است، یک حلقه برای محاسبه هر درایه از آن ماتریس را اضافه کنیم پس میشود 3 حلقه تودرتو!!

برای متد transpose هم به راحتی یک دور کل درایه های آرایه ورودی میچرخیم و جای سطر و ستون که همان متغییر i و  j ماست را با اندیس j و  iعوض می کنیم.

تست برنامه ترانهاده و ضرب ماتریس در جاوا

کد زیر ماتریس a و b را با هم ضرب و در آخر ترانهاده ماتریس a را محاسبه میکند. در آخر همه نتایج را نمایش میدهد.

public static void main(String[] args) {
double[][] a = { { 1, 2, 3 }, { 4, 5, 6 }, { 9, 1, 3 } };
double[][] b = { { 5, 3, 3 }, { 1, 7, 6 }, { 8, 5, 4 } };

double[][] multiple = multiply(a, b);
System.out.println("multiple");
for (int i = 0; i < multiple.length; i++) {
System.out.println(Arrays.toString(multiple[i]));

}

double[][] transpose = transpose(a);

System.out.println("matrix 'a' transpose");
for (int i = 0; i < transpose.length; i++) {
System.out.println(Arrays.toString(transpose[i]));

}



}

خروجی برنامه به صورت زیر است:

multiple
[31.0, 32.0, 27.0]
[73.0, 77.0, 66.0]
[70.0, 49.0, 45.0]
matrix 'a' transpose
[1.0, 4.0, 9.0]
[2.0, 5.0, 1.0]
[3.0, 6.0, 3.0]