در این جلسه تیم کدگیت را با آموزش درخت جستجوی دودویی در جاوا با همراهی کنید. پیش نیاز این قسمت شامل موارد زیر است:
- آشنایی با متد
- آشنایی با if
- آشنایی با for
- آشنایی با شی گرایی
- آشنایی با constructor
- آشنایی با this
- آشنایی با while
درخت جستجوی دودویی
درختی دودویی است که برای هر گره آن شروط زیر برقرار هستند:
1- مقادیر تمامی گرههای زیردرخت راست از مقدار گره بزرگتر هستند.
2- مقادیر تمامی گرههای زیردرخت چپ از مقدار گره کوچکتر هستند.

درج گره جدید در BST
برای اینکه یک گره جدید در درخت جستجوی دودویی اضافه کنیم، باید مکان آن را پیدا کنیم. برای یافتن محل مناسب، عملیات جستجو را برای آن (فرض می کنیم گره وجود دارد) انجام میدهیم. در آخر به گرهی خواهیم رسید که حداقل یکی از فرزندان آن تهی است. این گره والد گره جدید خواهد بود.
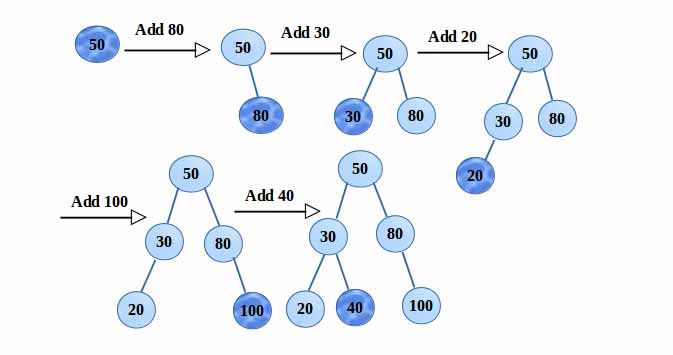
حذف گره از BST
حذف گره از درخت جستجوی دودویی به سه طریق انجام میگیرد:
1.گره برگ باشد که به راحتی قابل حذف از درخت میباشد
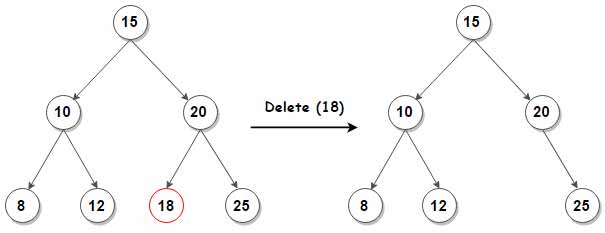
2.گره ما یک فرزند دارد. در این صورت گره حذف و فرزند آن جایگزین میشود.
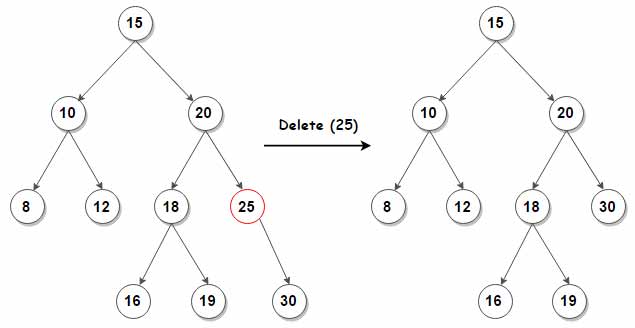
3.گره دارای دو فرزند است. ابتدا گرهی با کوچکترین مقدار در زیردرخت راست گره را پیدا میکنیم. درج این گره به جای گره قبلی شروط درخت جستجوی دودویی را به هم نمیزند. در نتیجه میتوان به راحتی آن را جایگزین کرد.
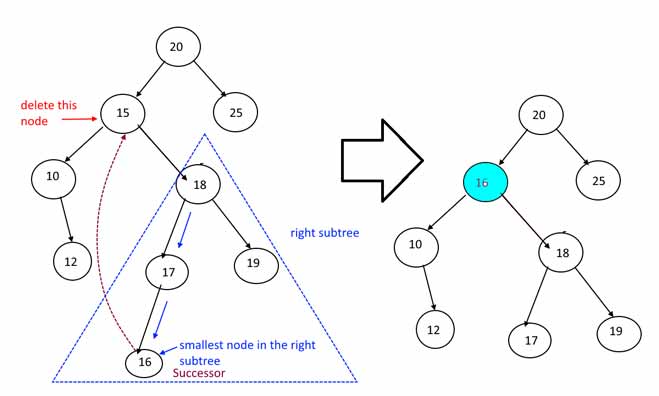
پیاده سازی درخت جستجوی دودویی در جاوا
برای پیاده سازی درخت دودویی در جاوا ابتدا باید یک کلاس برای نگهداری مقدار هر گره و فرزندان چپ و راست آن داشته باشیم.کلاس Node همین کار را برای ما میکند.
public class Node {
int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
کلاس Node شامل سه فیلد key و left و right است. در این کلاس یک constructor است که مقدار key را معین میکند.
بعد از ساخت هر گره نیاز به ساخت درخت است که ما کلاس BST را برای این کار در نظر گرفتیم.
public class BST {
Node root;
BST() {
root = null;
}
}
درخت ما نیاز به یک ریشه دارد که با آن به بقیه گره ها دسترسی پیدا کنیم. ما فیلد root را در درخت برای ارجاع به ریشه قرار دادیم. در این کلاس ما باید عملیات هایی که توضیح داده شد را پیاده سازی کنیم.
کد درج درBST (جاوا)
برای درج در درخت ابتدا باید به محلی برویم که میتوان گره را در آن قرار داد(در بالا توضیح داده شده است).متد insert برای درج در درخت است و کد آن به صورت زیر است.
void insert(int key) {
root = insertRec(root, key);
}
Node insertRec(Node root, int key) {
if (root == null) {
root = new Node(key);
return root;
}
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
return root;
}
همانطور که از کد درخت جستجوی دودویی در جاوا پیداست ابتدا چک میکنیم درخت ما خالی است یا خیر! اگر خالی بود ما ریشه را میسازیم.
if (root == null) {
root = new Node(key);
return root;
}
اگر درخت ما تعدادی گره داشت ما نیاز به پیدا کردن محل مناسب برای درج گره جدید داریم.
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
return root;
کد حذف گره در BST (جاوا)
برای حذف همانطور که گفته شد ما باید سه مرحله را طی کنیم. مرحله اول آن است که ما گره ای بدون فرزند را بخواهیم حذف کنیم و مرحله دو اگر یک فرزند داشته باشد و مرحله سه اگر دو فرزند داشته باشد. متد delete کد حذف را در سه مرحله به ما نشان میدهد.
void delete(int key) {
root = deleteRec(root, key);
}
Node deleteRec(Node root, int key) {
if (root == null)
return root;
if (key < root.key)
root.left = deleteRec(root.left, key);
else if (key > root.key)
root.right = deleteRec(root.right, key);
else {
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
root.key = minValue(root.right);
root.right = deleteRec(root.right, root.key);
}
return root;
}
int minValue(Node root) {
int minv = root.key;
while (root.left != null) {
minv = root.left.key;
root = root.left;
}
return minv;
}
همانطور که در کد میبینید ما ابتدا بررسی میکنیم آیا گره ای که میخواهیم وجود دارد یا خیر! در صورت درستی سه قسمتی که در قسمت حذف یک گره توضیح داده شد را انجام میدهیم
پیمایش BST (جاوا)
در این قسمت ما پیمایش inorder در درخت جستجوی دودویی را پیاده سازی خواهیم کرد. این پیمایش به این صورت است که ابتدا فرزند چپ یک گره را چاپ و بعد خود گره و در آخر فرزند راست گره را چاپ میکند. در درخت جستجو دودویی اگر از پیمایش inorder استفاده کنیم گره ها به صورت کوچک به بزرگ نمایش داده میشوند(چرا؟). برای پیاده سازی این پیمایش ما از روش بازگشتی استفاده کردیم. کد این پیمایش به صورت زیر است:
void inorder() {
inorderRec(root);
}
void inorderRec(Node root) {
if (root != null) {
inorderRec(root.left);
System.out.println(root.key);
inorderRec(root.right);
}
}
تست برنامه درخت جستجوی دودویی در جاوا
این قسمت برای کد خود یک main مینویسیم. کد زیر main برنامه درخت جستجوی دودویی است.
public static void main(String[] args) {
BST tree = new BST();
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
System.out.println(
"Inorder traversal of the given tree");
tree.inorder();
System.out.println("\nDelete 20");
tree.delete(20);
System.out.println(
"Inorder traversal of the modified tree");
tree.inorder();
}












سلام
مرسی از اموزشی که دادید
میخواستم ببینم برای این که یک عبارت محاسباتی را پیمایش کنیم باید چیکار کنیم مثلا عبارت inorder باشه بعد تبدیل به postorder , preorder بشه
اگه لطف کنیم کدشو به java برام بگید خیلی ممنون میشم