در این قسمت تیم کدگیت را با آموزش درخت AVL در پایتون همراهی کنید. در این جلسه به معرفی یکی دیگر از ساختار دادهها خواهیم پرداخت. با معرفی درخت AVL کار خود را آغاز کرده و در ادامه به پیاده سازی این درخت در پایتون خواهیم پرداخت. پیشنهاد میکنیم قبل از مطالعه این جلسه، آموزشهای زیر را بررسی کنید:
- درخت دودویی جست جو در پایتون
- تابع در پایتون
- آشنایی با روش بازگشتی
- آشنایی با if
- آشنایی با for
- While در پایتون
درخت AVL
عملیاتهای درج گره و حذف گره در درخت دودویی جستجو به طور معمول O(logn) است. اما درخت جستجوی دودویی زیر را ببینید:
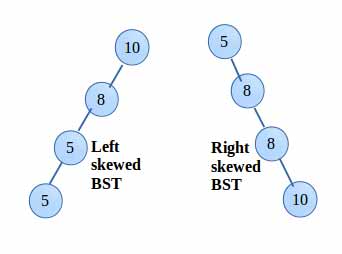
در این شرایط حذف و اضافه کردن گره زمان O(n) میگیرد. اگر در درخت فوق پس از هر حذف و یا اضافه کردن درخت، ما تضمین کنیم ارتفاع درخت log n است پس هزینه درج و حذف همانطور که انتظار داریم Log n خواهد بود (در بدترین حالت). درخت AVL نوعی درخت جستجوی باینری با ارتفاع متعادل است بدین معنی که تضمین میکند ارتفاع درخت همیشه O(logn) است.
در این آموزش تنها به توضیح و پیاده سازی عملیات درج گره در درخت AVL خواهیم پرداخت. در جلسات آینده عملیاتهای مانند حذف و … نیز توضیح داده میشود.
درج گره در درخت AVL
برای درج گره در درخت AVL ابتدا همانند BST عمل کرده و گره را در درخت درج میکنیم. سپس با عملیاتی (که توضیح خواهیم داد) ارتفاع درخت را متعادل میکنیم. برای متعادل کردن ارتفاع درخت AVL ما نیاز به عملیاتهایی به نام چرخش راست و چرخش چپ داریم. تصویر زیر این چرخشها را به صورت ساده نمایش داده است:
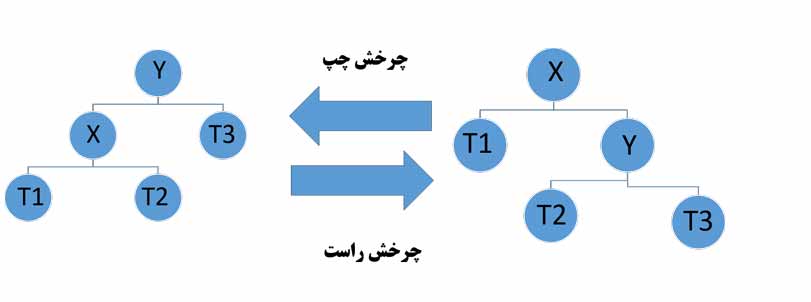
مطابق با تصویر فوق متغیرهای T1 و T2 و T3 فرزندان درختی هستند که ریشه آن گره X یا Y است. دقت کنید چرخش چپ و راست به صورت همزمان در یک تصویر آورده شده است.
برای درج گره در درخت AVL، مانند درخت BST عمل کرده و گره را وارد درخت میکنیم. پس از وارد کردن گره بررسی میکنیم درخت ما شرط AVL را دارد (متعادل هست یا خیر). برای ایجاد تعادل در درخت AVL حالات زیر در درخت رخ خواهد داد:
- Y فرزند چپ z و x فرزند چپ y است:
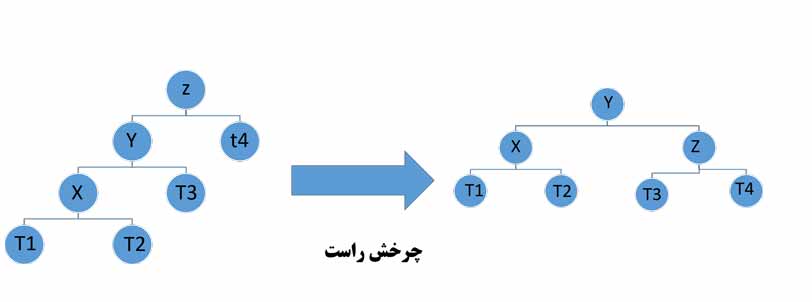
- Y فرزند چپ z و x فرزند راست y است:
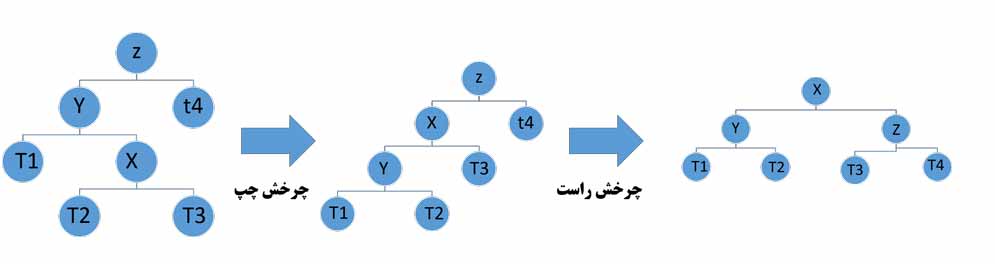
- Y فرزند راست z و x فرزند راست y است:
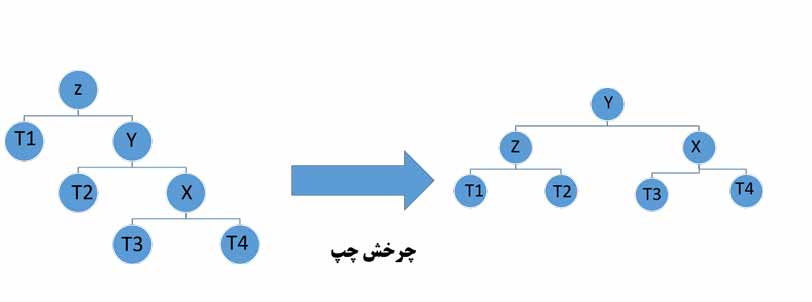
- Y فرزند راست z و x فرزند چپ y است:
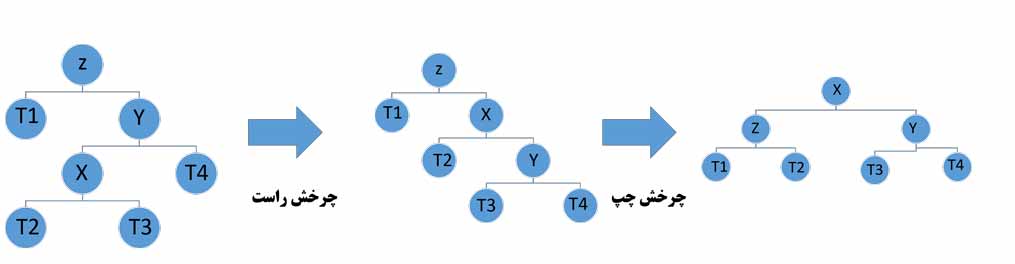
پیاده سازی درخت AVL در پایتون
برای پیاده سازی درخت AVL در پایتون همانند پیاده سازی درخت BST یک کلاس Node ایجاد میکنیم(در اینجا نام کلاس TreeNode قرار دادیم). سورس این کلاس مانند درخت BST بوده و تنها برای نگهداری ارتفاع گرهها متغیری به نام Height به آن اضافه کردیم. کد کلاس TreeNode به صورت زیر است:
class TreeNode(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.height = 1
حال نوبت به پیاده سازی درخت است. ابتدا کد درخت AVL را با هم ببینیم:
class AVL_Tree(object):
def insert(self, root, key):
if not root:
return TreeNode(key)
elif key < root.val:
root.left = self.insert(root.left, key)
else:
root.right = self.insert(root.right, key)
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
balance = self.getBalance(root)
# Case 1 - Left Left
if balance > 1 and key < root.left.val:
return self.rightRotate(root)
# Case 2 - Right Right
if balance < -1 and key > root.right.val:
return self.leftRotate(root)
# Case 3 - Left Right
if balance > 1 and key > root.left.val:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
# Case 4 - Right Left
if balance < -1 and key < root.right.val:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def rightRotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def getHeight(self, root):
if not root:
return 0
return root.height
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def inOrder(self, root):
if not root:
return
self.inOrder(root.left)
print("{0} ".format(root.val), end="")
self.inOrder(root.right)
توابع و متغیرهای استفاده شده در کد بالا به صورت زیر میباشد:
- تابع getHeight: ارتفاع یک گره در درخت را برمیگرداند.
- تابع insert: تابع insert به صورت بازگشتی یک گره را در دخت اضافه میکند.
- تابع getBalance: این تابع یک گره را به عنوان ورودی میگیرد و اختلاف زیردرخت راست و چپ آن را برمیگرداند. وقتی این تابع عدد بزرگتر از 1 را برمیگرداند بدین معنی است که درخت متعادل نیست و ما با چرخش (چرخش راست یا چرخش چپ سپس چرخش راست) نیاز داریم. در صورتی که عدد کوچکتر از -1 برگردانده شود یعنی ما در شرایط عکس حالت قبل هستیم.
- تابع leftRotate: این تابع چرخش چپ را انجام میدهد.
- تابع rightRotate: این تابع چرخش راست را انجام میدهد.
- تابع Inorder: این تابع برای پیمایش درخت میباشد. از این متد برای چاپ گرههای درخت در این مثال استفاده خواهد شد.
تست برنامه
برای تست کدهای بالا، کد زیر را پیاده سازی کنید:
myTree = AVL_Tree()
root = None
root = myTree.insert(root, 10)
root = myTree.insert(root, 20)
root = myTree.insert(root, 30)
root = myTree.insert(root, 40)
root = myTree.insert(root, 50)
root = myTree.insert(root, 25)
print("inOrder traversal of the",
"constructed AVL tree is")
myTree.inOrder(root)
print()
خروجی کد بالا به صورت زیر است:
Preorder traversal of the constructed AVL tree is
10 20 25 30 40 50
اگر سوالی در خصوص درخت AVL دارید در قسمت کامنت سوال خود را مطرح کنید تا پاسخگوی شما باشیم.














کمترین و بیشترین ارتفاع درخت avl وقتی درخت ۱۰هزارکلید را در خود ذخیره کرده است چه می شود؟
سلام. ارتفاع درخت log n است. n در اینجا تعداد نود است. برای شما n برابر با 10 هراز است.