الگوریتم KMP در جاوا (KMP Algorithm)

مارس 24, 2024
ارسال توسط سعید غریبی

در این قسمت تیم کدگیت را با آموزش الگوریتم KMP در جاوا همراهی کنید. در ابتدای آموزش در مورد تطابق رشته‌ها صحبت کرده و سپس الگوریتم KMP را معرفی می‌کنیم. در پایان با توجه به پیچیدگی این الگوریتم، به پیاده سازی آن در زبان جاوا خواهیم پرداخت. پیشنهاد می‌کنیم قبل از مطالعه این جلسه، آموزش‌های زیر را مطالعه کنید:

الگوریتم KMP در جاوا

الگوریتم جستجوی رشته (و یا تطبیق رشته‌ها) به رده مهمی از الگوریتم‌های موجود در رابطه با رشته‌ها اطلاق می‌شود. همانطور که از عنوانشان مشخص است، برای پیدا کردن یک رشته در میان یک متن بکار می‌روند و مکان آن رشته بخصوص را در متن مشخص می‌کنند و همچنین کاربرد بسیاری از جمله در جستجوهای اینترنتی دارند(ویکیپدیا).

الگوریتم KMP بر خلاف الگوریتم Naïve برای جستجوی در رشته از آرایه‌ای برای ذخیره حالت‌های قبل کمک می‌گیرد. هر دو الگوریتم به دنبال جستجوی رشته ورودی (Pattern) درون متن هستند.

در روشی که در این قسمت ارائه می‌دهیم الگوریتم KMP را با کمک DFA پیاده سازی می‌کنیم. ایده برنامه ما بدین صورت است که قبل از جستجو به روش KMP، یک DFA بر اساس pattern ورودی بسازیم سپس با کمک آن، الگوریتم kmp را پیاده‌سازی کنیم. همچنین قبل از پیاده سازی این الگوریتم، نحوه ساخت DFA بر اساس pattern ورودی را توضیح می‌دهیم.

ساخت DFA بر اساس رشته Pattern

برای ساخت DFA ابتدا یک آرایه دو بعدی به اندازه m*n می‌سازیم که m تعداد حروف یا کلمات الفبا مورد استفاده ما در برنامه است و n طول رشته Pattern می‌باشد. حال همانطور که می‌دانید DFA پس از دریافت یک رشته حالت بعدی برنامه را مشخص می‌کند. برنامه ما آرایه‌ای شبیه به تصویر زیر در ابتدا ایجاد می‌کند:

همانطور که می‌بینید ستون‌ها Pattern ما هستند و سطرها حروف الفبای ما می‌باشد. حال اگر در متن ورودی توسط کاربر حرف A بیاید و ما در ستون با اندیس دو باشیم چه اتفاقی رخ می‌دهد؟ کاملا درست است باید به مرحله بعدی یعنی ستون با اندیس سه برویم. همانطور که میبینید با داشتن آرایه DFA کاملا راحت می‌توان پاسخ مسئله رسید. دیاگرام DFA آرایه بالا به صورت زیر می‌باشد(توضیح دیاگرام زیر بر عهده خواننده محترم!!).

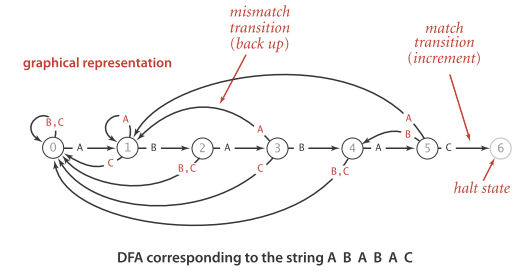
ساخت آرایه DFA

حال تا این قسمت ما متوجه شدیم با استفاده آرایه DFA میتوانیم الگوریتم KMP را حل کنیم. اما چگونه آرایه DFA را بر اساس Pattern ورودی بسازیم؟ برای این کار ما حالات مختلف زیر را در نظر می‌گیریم:

حالت تطابق: وقتی کلمه وارد شده به DFA ما را به حالت بعد (یک قدم به پایان نزدیکتر کردن) ببرد.
حالت عدم تطابق: وقتی کلمه وارد شده به DFA ما را به عقب برگرداند.

حالت تطابق بسیار ساده می‌باشد. و به راحتی در آرایه می‌توان جایگزین کرد و آرایه DFA را ساخت. اما حالت عدم تطابق چگونه است و برای آن چه اتفاقی می‌افتد. برای حل عدم تطابق به مقایسه آرایه زیر دقت کنید. همانطور که می‌بینید مقادیر عدم تطابق دقیقا شبیه به یکی از حالت‌های قبلی آرایه ما است. اما چگونه حالت قبلی را بدست بیاوریم تا بتوانیم درون آرایه قرار دهیم؟

همانطور که در تصویر می‌بینید اشاره‌گری به نام X وجود دارد که ما آن را اشاره‌گر عدم تطابق می‌نامیم. این اشاره‌گر حالت‌های عدم تطابق را برای ما پیدا می‌کند. فقط دقت شود که وقتی ما در حال پر کردن آرایه هستیم زمانی که وارد ستون(اندیس) اول آرایه شدیم این اشاره‌گر وارد برنامه یا ستون(اندیس) صفر می‌شود. وقتی در حال پر کردن Current State یا وضعیت فعلی هستیم در صورت برخورد با عدم تطابق به X رجوع می‌کنیم. همچنین برای رفتن وضعیت بعدی در این مثال (تصویر بالا اولین آرایه) ستون دوم، باید ببینیم با چه حرفی به وضعیت دو میرویم (حرف B) سپس بررسی کنیم با ورودی B اشاره‌گر X به کدام ستون می‌رود (در تصویر بالا همان ستون صفر باقی می‌ماند).

پیاده‌سازی الگوریتم KMP در جاوا

این قسمت با کمک توضیحات بالا به پیاده سازی‌الگوریتم KMP در جاوا می‌پردازیم. همانطور که توضیح دادیم ما نیاز به آرایه DFA داریم. برای پیاده سازی ما کلاسی به نام KMP ایجاد کرده و در Constructor آن، رشته pattern را در ورودی دریافت و آرایه DFA در آن ساختیم. در زیر کد Constructor آورده شده است:

    public KMP(String pat) {

        this.R = 256;

        this.pat = pat;



        // build DFA from pattern

        int m = pat.length();

        dfa = new int[R][m];

        dfa[pat.charAt(0)][0] = 1;

        for (int x = 0, j = 1; j < m; j++) {

            for (int c = 0; c < R; c++)

                dfa[c][j] = dfa[c][x];     // Copy mismatch cases.

            dfa[pat.charAt(j)][j] = j+1;   // Set match case.

            x = dfa[pat.charAt(j)][x];     // Update restart state.

        }

    }

متغیر R در کد بالا همان تعداد حروف الفبای ما است که 256 فرض کرده‌ایم. همانطور که در کد بالا می‌بینید دو حالت برای ساخت DFA توضیح داده‌ایم، آورده شده است. یکی حالت عدم تطابق(حلقه For دوم) و دیگری حالت تطابق(در کامنت نوشته شده Set Match Case). در آخر کد به بروزرسانی اشاره‌گر X پرداخته‌ایم. حال کد KMP را بررسی کنیم:

    public int search(String txt) {



        // simulate operation of DFA on text

        int m = pat.length();

        int n = txt.length();

        int i, j;

        for (i = 0, j = 0; i < n && j < m; i++) {

            j = dfa[txt.charAt(i)][j];

        }

        if (j == m) return i - m;    // found

        return n;                    // not found

    }

در کد بالا با دریافت متن ورودی کاربر، به جست‌جوی pattern در آن می‌پردازیم. در حلقه for بالا با توجه به متن ورودی کاربر به کمک آرایه DFA متغیر j را بروزرسانی می‌کنیم وقتی این متغیر به اندازه طول pattern باشد یعنی جستجو موفق آمیز بوده و ما اندیس کلمه پیدا شده درون آرایه ورودی را بر‌می‌گردانیم.

تست الگوریتم KMP در جاوا

برای تست کدهای بالا، کد main زیر را بزنید:

 public static void main(String[] args) {

        String pat = "abracadabra";

        String txt = "abacadabrabracabracadabrabrabracad";

        KMP kmp1 = new KMP(pat);

        int offset1 = kmp1.search(txt);



        System.out.println("text:    " + txt);



        System.out.print("pattern: ");

        for (int i = 0; i < offset1; i++)

        System.out.print(" ");

        System.out.println(pat);

    }

}

خروجی کد بالا به صورت زیر می‌باشد:

text: abacadabrabracabracadabrabrabracad

pattern: abracadabra