جستجوی اول سطح در جاوا (Breadth First Search)

در این جلسه تیم کدگیت را با آموزش جستجوی اول سطح در جاوا همراهی کنید. این آموزش پیش نیازهای زیر را دارد:

1. رابط برنامه نویسی گراف
2. پشته
3. صف
4. آشنایی با گراف
5. آشنایی با لیست پیوندی در جاوا
6. Iterator در جاوا
7. آشنایی با This در جاوا
8. آشنایی با Constructor در جاوا
9. آشنایی با متد در جاوا
10. آشنایی با آرایه
11. آشنایی با خواندن و نوشتن فایل در جاوا
12. حلقه while در جاوا
13. آشنایی مدیریت استثناها
14. آشنایی با if
15. آشنایی به for
16. آشنایی با شی گرایی

اگر با مطالب بالا آشنا نیستید در آموزش های قبل درباره این مطالب صحبت شده است بنابراین پیشنهاد میشود مطالب بالا را بخوانید و سپس به مطالعه این آموزش بپردازید.

جستجوی اول سطح

در نظریه گراف، جستجوی اول سطح یکی از الگوریتم‌های پیمایش گراف است. استراتژی جستجوی سطح اول برای پیمایش گراف، همانطور که از نامش پیداست «جستجوی سطح به سطح گراف» است.

الگوریتم از ریشه شروع می‌کند (در گراف‌ها و یا درخت‌های بدون ریشه رأس دلخواهی به عنوان ریشه انتخاب می‌شود) و آن را در سطح یک قرار می‌دهد. سپس در هر مرحله همه همسایه‌های رئوس آخرین سطح دیده شده را که تا به حال دیده نشده‌اند بازدید می‌کند و آنها را در سطح بعدی می‌گذارد. این فرایند زمانی متوقف می‌شود که همه همسایه‌های رئوس آخرین سطح قبلاً دیده شده باشند. همچنین در مسائلی که حالات مختلف متناظر با رئوس یک گراف‌اند و حل مسئله مستلزم یافتن رأس هدف با خصوصیات مشخصی است که در عین حال در بین همه رئوس هدف با آن خصوصیات به ریشه نزدیک‌ترین باشد، جستجوی سطح اول به صورت غیرخلاق عمل می‌کند. بدین ترتیب که الگوریتم هر دفعه همه همسایه‌های یک رأس را بازدید کرده و سپس به سراغ رأس بعدی می‌رود و بنابراین گراف سطح به سطح پیمایش خواهد شد. این روند تا جایی ادامه می‌یابد که رأس هدف پیدا شود و یا احتمالاً همه گراف پیمایش شود. براساس آنچه گفته شد پیاده‌سازی هوشمندانه الگوریتم آنقدر مؤثر نخواهد بود.

از نقطه نظر عملی، برای پیاده‌سازی این الگوریتم از صف استفاده می‌شود. بدین ترتیب که در ابتدا ریشه در صف قرار می‌گیرد. سپس هر دفعه عنصر ابتدای صف بیرون کشیده شده، همسایگانش بررسی شده و هر همسایه‌ای که تا به حال دیده نشده باشد به انتهای صف اضافه می‌شود. جزئیات پیاده‌سازی در ادامه خواهد آمد(ویکیپدیا)

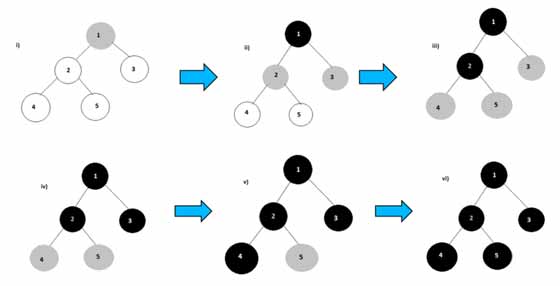
جستجوی اول سطح در جاوا

برای پیاده سازی جستجوی اول سطح در جاوا همانطور که گفته شد از صف استفاده میکنند. ما قبلا صف در جاوا را پیاده سازی کردیم و از همان صف استفاده میکنیم.نکته بعدی این است که ما از گراف استفاده میکنیم و در آموزش های قبل درباره رابط برنامه نویسی گراف توضیج دادیم. در کدی که به شما ارایه میدهیم از پشته نیز استفاده کردیم(در ادامه دلیل آن را میبینید).پشته را نیز قبلا پیاده سازی کردیم و از آن استفاده میکنیم (در کد پشته  اگر implement نمیکرد کلاسی را، شما به آن implements Iterable<Item>  اضافه کنید).

import java.io.File;
import java.io.FileNotFoundException;



public class BreadthFirstSearch {
     private static final int INFINITY = Integer.MAX_VALUE;
     private boolean[] marked; // marked[v] = is there an s-v path
     private int[] edgeTo; // edgeTo[v] = previous edge on shortest s-v path
     private int[] distTo; // distTo[v] = number of edges shortest s-v path


     public BreadthFirstSearch(Graph G, int s) {
          marked = new boolean[G.V()];
          distTo = new int[G.V()];
          edgeTo = new int[G.V()];
          bfs(G, s);

     }



     private void bfs(Graph G, int s) {
          Queue<Integer> q = new Queue<Integer>();
          for (int v = 0; v < G.V(); v++)
              distTo[v] = INFINITY;
          distTo[s] = 0;
          marked[s] = true;
          q.Enqueue(s);

          while (!q.isEmpty()) {
              int v = q.Dequeue();
              for (int w : G.adj(v)) {
                   if (!marked[w]) {
                        edgeTo[w] = v;
                        distTo[w] = distTo[v] + 1;
                        marked[w] = true;
                        q.Enqueue(w);
                   }
              }
          }
     }

     public boolean hasPathTo(int v) {
          return marked[v];
     }

     public int distTo(int v) {
          return distTo[v];
     }

     public Iterable<Integer> pathTo(int v) {
          if (!hasPathTo(v))
              return null;
          StackWithList<Integer> path = new StackWithList<Integer>();
          int x;
          for (x = v; distTo[x] != 0; x = edgeTo[x])
              path.push(x);
          path.push(x);
          return path;
     }

}

کد جستجوی اول سطح در جاوا فیلد های زیر را دارد:

1. Marked : این فیلد یک آرایه به تعداد راس هاست.اگر در جستجوی اول سطح راسی دیده شود مقدار اندیس آن true میشود.
2. INFINITY: این فیلد را همان عدد بی نهایت گذاشتیم و وقتی دو راس به هم مسیری ندارند فاصله آن را بینهایت قرار میدهیم.
3. EdgeTo: این آرایه نیز به تعداد راسهاست. اگر ما از راس 2 به راس 5 رسیده باشیم EdgeTo[5]=2 قرار میدهیم.(به طور کلی مسیر را نگه میدارد.)
4. DistTo : این آرایه نیز به تعداد راس هاست و فاصله هر راس از نقطه شروع را در خود ذخیره میکند.

متدهایی که در کد بالا استفاده شده :

1. BreadthFirstSearch: این متد constructor است و یک گراف و راس شروع را میگیرد و جستجوی اول سطح را شروع میکند.
2. Bfs: این متد جستجوی اول سطح در جاوا را پیاده سازی کرده. است. ابتدا distto همه راس ها را برابر بینهایت قرار میدهد. یک صف را میسازد و هر راسی که قبلا دیده نشده بود به صف اضافه میکند.
3. Haspathto: این متد به ما میگوید آیا از راس شروع تا راسی خاص (ورودی متد) مسیری وجود دارد یا خیر!
4. Disto: این متد به ما میگوید فاصله راس شروع تا راس خاص (ورودی متد) چقدر است.
5. PathTo: مسیر بین دو راس شروع و راس خاص (ورودی متد) را به میدهد.

تست جستجوی اول سطح در جاوا

برای تست جستجوی اول سطح در جاوا کد زیر را بزنید.

public static void main(String[] args) {

          Graph G = null;
          try {
              G = new Graph(new File("graph.txt"));
          } catch (FileNotFoundException e) {
              e.printStackTrace();
          }

          int s = 0;
          BreadthFirstSearch bfs = new BreadthFirstSearch(G, s);

          for (int v = 0; v < G.V(); v++) {
              if (bfs.hasPathTo(v)) {
                   System.out.print(s + " to " + v + " ( " + bfs.distTo(v)
                             + " )  ");
                   for (int x : bfs.pathTo(v)) {
                        if (x == s)
                             System.out.print(x);
                        else
                             System.out.print("-" + x);
                   }
                   System.out.println();
              }
          }

     }

در کد بالا فایل graph.txt به صورت زیر است:

6
8
0 5
2 4
2 3
1 2
0 1
3 4
3 5
0 2

خروجی برنامه نیز به صورت زیر است:

0 to 0 ( 0 )  0
0 to 1 ( 1 )  0-1
0 to 2 ( 1 )  0-2
0 to 3 ( 2 )  0-2-3
0 to 4 ( 2 )  0-2-4
0 to 5 ( 1 )  0-5